Optimal Prevention Of Reordering Attacks

05 May 2024 - Vincent

Although illegal on Wall Street, reordering attacks happen regularly on blockchains. With researchers from the University of Sydney, we recently solved this problem optimally even for networks where message delays are arbitrary [1]. The key idea is to combine threshold signatures with information dissemination to achieve optimal communication complexity. The scientific article will be published in the proceedings of the 54th IEEE/IFIP International Conference on Dependable Systems and Networks (DSN) in Brisbane, Australia in June 2024.

Between 2020 and 2022, opportunistic traders have extracted hundreds of millions of dollars by including, excluding, and changing the order of decentralized finance (DeFi) transactions [2]. The crux of the problem is that blockchains order transactions in any consistent order, regardless of the order in which these transactions are received. In particular, front-running [3], which is an illegal trading strategy whereby a privileged player makes a profit by exploiting non-public information, is regularly executed on blockchains due to the lack of ordering solutions.

The ordering attempts to solve this problem either make use of commit-reveal to obfuscate the transaction payloads prior to ordering them or offer a fair ordering with a cubic communication complexity. These solutions are impractical for the blockchains that tend to scale to a large number of nodes. Relative and absolute ordering strategies have been proposed, however, the former suffers from cyclic dependencies while the latter cannot work in networks where the time it takes to deliver a message can be arbitrary.

Our new solution, called Asynchronous Ordered Atomic Broadcast (AOAB) solves the remaining problem of cyclic dependencies and message delays. To this end, AOAB makes use of threshold signatures and information dissemination to reach a communication complexity of $O(nl + λn^2)$, where $n$ is the number of nodes ordering transactions, $l$ is the input (transaction) size and $λ$ is the security parameter, as depicted in the figure below. This is optimal when $l ≥ λn$.

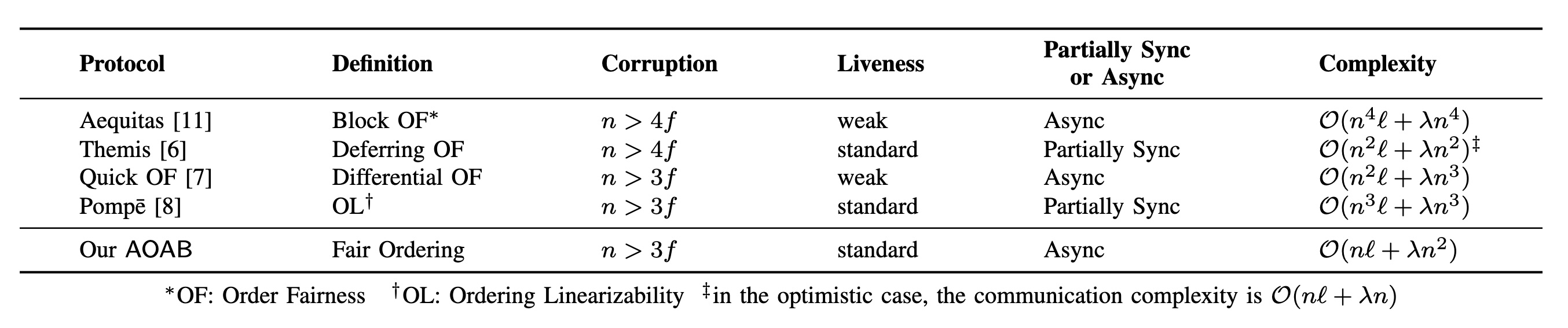
More precisely, AOAB exploits threshold signatures to reduce the cost by an extra linear multiplicative factor. In addition, to prevent Byzantine nodes from blowing up the cost per transaction, AOAB applies data dissemination that distributes the output transactions to all nodes. Finally, AOAB is resilience optimal, tolerating $f < n/3$ Byzantine nodes.

AOAB proceeds in consecutive epochs, during each epoch all correct nodes output the same set of transactions in the same order. Each transaction is output with a unique sequence number used to order the transactions in the epoch. The set of transactions output during each epoch sequentially extends the output of the state machine replication.

Each epoch is divided into an ordering phase and an agreement phase. During the ordering phase, the issuer of each transaction $t$ collects a set $S$ of $2f+1$ distinct sequence numbers, builds a threshold signature $Σ$ for the median value $s$ of $S$, and broadcasts $t$, $s$ and $Σ$. Then, during the agreement phase, processes agree on a set of transactions and associated sequence numbers { $t,s,Σ$ } that are output for the current epoch. The fact that $s$ is the median value of a set of size $2f + 1$ ensures that $s$ is upper bounded and lower bounded by values of sequence numbers assigned to $t$ by correct processes. The signature $Σ$ proves the value of $s$ while keeping communication optimal.

To conclude, AOAB combines cryptography with broadcast protocols to devise the first asynchronous order-fair protocol with optimal communication complexity and optimal fault tolerance.

[1] V. Gramoli, Z. Lu, Q. Tang, P. Zarbafian. AOAB: Optimal and Fair Ordering of Financial Transactions. 54th IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), 2024.

[2] K. Qin, L. Zhou, and A. Gervais. Quantifying blockchain extractable value: How dark is the forest?. IEEE Symposium on Security and Privacy (SP), 2022, pp. 198–214.

[3] S. Eskandari, S. Moosavi, and J. Clark. Transparent dishonesty: front-running attacks on blockchain. 3rd Workshop on Trusted Smart Contracts (WTSC), 2019.